The DS data structure is a general purpose bucket of GAUSS types.  It contains one of each of the types, matrix, array, string, string array, sparse matrix, and scalar.  It is passed to the log-likelihood procedure untouched by cmlmt.  It can be used by programmers in any way they choose to help in computing the log-likelihood.  Typically it is used to pass data to the procedure.  The DS structure can also be reshaped into a vector of structures giving the programmer great flexibility in handling data and other information.
load x[200,5] = data.csv;

struct DS d0;

// creates a 2x1 vector of
// default data structures
d0 = reshape(dsCreate,2,1);  

// dependent variable
d0[1].dataMatrix = x[.,1];   

// independent variables
d0[2].dataMatrix = x[.,2:4];


This structure handles the matrices and strings that control the estimation process such as setting the descent algorithm, the line search method, and so on.  It is also used to specify the constraints.  For example the thresholds need to be constrained in the following way where .  This implies the two free constraints

The programmer will accomplish by specifing two members of the cmlmtControl structure, C and D, to impose this inequality constraint

where x is the vector of parameters being estimated.  Then

struct cmlmtControl c0;

// creates a default structure
c0 = cmlmtControlCreate;

c0.C = { 0  0  0 -1  1  0,
         0  0  0  0 -1  1 };

c0.D = { 0,
         0 };

The first three columns of the matrix c0.C and the vector c0.D are associated with regression coefficients that are unconstrained and the last two are associated with the thresholds.

The Log-likelihood Procedure

The programmer now writes a GAUSS procedure computing a vector of log-likelihood probabilities.  This procedure has three input arguments, the PV parameter structure, the DS data structure, and 3×1 vector the first element of which is nonzero if cmlmt is requesting the vector of log-likelihood probabilities, the second element nonzero if it is requesting the matrix of first derivatives with respect to the parameters, and the third element nonzero if it is requesting the Hessian or array of second derivatives with respect to the parameters.  It has one return argument, a modelResults structure containing the results.

proc orderedProbit(struct PV p, struct DS d, ind);
   local mu, tau, beta, emu, eml;
   struct modelResults mm;

   if ind[1] == 1;
      tau = pvUnpack(p,”tau”);
      beta = pvUnpack(p,”beta”);
      mu = d[2].dataMatrix * beta;
      eml = submat(tau,d[1].dataMatrix,0) – mu;
      emu = submat(tau,d[1].dataMatrix + 1,0) – mu;
      mm.function = ln(cdfn(emu) – cdfn(eml));
   endif;
retp(mm);
endp;

The GAUSS submat function serves to pull out the k-th element of tau for the i-th row of d[1].datamatrix set to k.

Since this procedure doesn’t return a matrix of first derivatives nor an array of second derivatives they will be computed numerically by cmlmt.

The result stored in mm.function is an Nx1 vector of log-probabilities computed by observation.  If we were to have provided analytical derivatives, the first derivatives would be an Nxm matrix of derivatives computed by observation where m is the number of parameters to be estimated, and the second derivatives would be an Nxmxm array of second derivatives computed by observation.  Computing these quantities in this way improves accuracy.  It also allows for the BHHH descent method which is more accurate than other methods permitting a larger convergence tolerance.

It is also possible to return a scalar log-likelihood which is the sum of the individual log-probabilities.  In this case the analytical first derivatives would be a 1xm gradient vector, and the second derivatives a 1xmxm array.  You would also need to set c0.numObs to the number of observations since cmlmt is no longer able to determine the number of observations from the length of the vector of log-probabilities.

The Command File

Finally we put it all together in the command file:

library cmlmt;

// contains the structure definitions
#include cmlmt.sdf;  

// simulating data here
x = rndn(200,3);
b = { .4, .5, .6 };
ystar = x*b;
tau = { -50, -1, 0, 1, 50 };

y = (ystar .> tau[1] .and ystar .<= tau[2]) +
   2 * (ystar .> tau[2] .and ystar .<= tau[3]) +
   3 * (ystar .> tau[3] .and ystar .<= tau[4]) +
   4 * (ystar .> tau[4] .and ystar .<= tau[5]);

struct DS d0;

// creates a 2x1 vector of
// default data structures
d0 = reshape(dsCreate,2,1);  

// dependent variable
d0[1].dataMatrix = y; 

// independent variables
d0[2].dataMatrix = x; 

struct PV p0;

// creates a default parameter structure
p0 = pvCreate;

p0 = pvPack(p0,.5|.5|.5,"beta");
p0 = pvPackm(p0,-30|-1|0|1|30,"tau",0|1|1|1|0);

struct cmlmtControl c0;

// creates a default structure
c0 = cmlmtControlCreate; 

c0.C = { 0  0  0 -1  1  0,
         0  0  0  0 -1  1 };

c0.D = { 0,
         0};

struct cmlmtResults out;

out = cmlmt(&orderedProbit,p0,d0,c0);

// prints the results
call cmlmtprt(out);

proc orderedProbit(struct PV p, struct DS d, ind);
   local mu, tau, beta, emu, eml;
   struct modelResults mm;

   if ind[1] == 1;
      tau = pvUnpack(p,"tau");
      beta = pvUnpack(p,"beta");
      mu = d[2].dataMatrix * beta;
      eml = submat(tau,d[1].dataMatrix,0) - mu;
      emu = submat(tau,d[1].dataMatrix + 1,0) - mu;
      mm.function = ln(cdfn(emu) - cdfn(eml));
   endif;

retp(mm);
endp;

This program produces the following output:

================================================================

CMLMT Version 2.0.7         3/30/2012   1:29 pm

=================================================================

return code =    0

normal convergence

Log-likelihood        -15.1549

Number of cases     200

Covariance of the parameters computed by the following method:

ML covariance matrix

Parameters    Estimates     Std. err.  Est./s.e.  Prob.    Gradient

------------------------------------------------------------------

beta[1,1]    4.2060        0.2385      17.634   0.0000      0.0000

beta[2,1]    5.3543        0.2947      18.166   0.0000      0.0000

beta[3,1]    6.2839        0.2789      22.531   0.0000      0.0000

tau[2,1]   -10.7561        0.7437     -14.462   0.0000      0.0000

tau[3,1]    -0.0913        0.2499      -0.365   0.7148      0.0000

tau[4,1]    10.6693        0.5697      18.727   0.0000      0.0000

Correlation matrix of the parameters

1     0.52064502     0.54690534    -0.46731768    0.046211496    0.57202935

0.52064502     1     0.58363048    -0.47574225   -0.061765839    0.65959766

0.54690534     0.58363048     1    -0.5169026    -0.0059238287   0.69077806

-0.46731768   -0.47574225    -0.5169026      1    0.0046253798  -0.44858539

0.046211496  -0.061765839   -0.0059238287   0.0046253798    1  -0.01457591

0.57202935    0.65959766     0.69077806    -0.44858539     -0.01457591   1

Wald Confidence Limits

0.95 confidence limits

Parameters    Estimates     Lower Limit   Upper Limit   Gradient

----------------------------------------------------------------------

beta[1,1]    4.2060        3.7355        4.6764        0.0000

beta[2,1]    5.3543        4.7730        5.9356        0.0000

beta[3,1]    6.2839        5.7338        6.8339        0.0000

tau[2,1]   -10.7561      -12.2230       -9.2893        0.0000

tau[3,1]    -0.0913       -0.5842        0.4015        0.0000

tau[4,1]    10.6693        9.5457       11.7929        0.0000

Number of iterations    135

Minutes to convergence     0.00395

Constrained Optimization MT (COMT) solves the Nonlinear Programming problem, subject to general constraints on the parameters – linear or nonlinear, equality or inequality, using the Sequential Quadratic Programming method in combination with several descent methods selectable by the user:

• Newton-Raphson
• quasi-Newton (BFGS and DFP)
• Scaled quasi-Newton

There are also several selectable line search methods. A Trust Region method is also available which prevents saddle point solutions. Gradients can be user-provided or numerically calculated. COMT is fast and can handle large, time-consuming problems because it takes advantage of the speed and number-crunching capabilities of GAUSS. It is thus ideal for large scale Monte Carlo or bootstrap simulations.

New Features

• Internally threaded functions
• Uses structures
• Improved algorithm
• Allows for computing a subset of the derivatives analytically, and for combining the calculation of the function and derivatives, thus reducing calculations in common between function and derivatives

Threading in COMT

If you have a multi-core processor you may take advantage of COMT’s internally threaded functions. An important advantage of threading occurs in computing numerical derivatives. If the derivatives are computed numerically, threading will significantly decrease the time of computation.


Example

We ran a time trial of a covariance-structure model on a quad-core machine. As is the case for most real world problems, not all sections of the code are able to be run in parallel. Therefore, the theoretical limit for speed increase is much less than (single-threaded execution time)/(number of cores).

Even so, the execution time of our program was cut dramatically:

Single-threaded execution time: 35.42 minutes
Multi-threaded execution time: 11.79 minutes

That is a nearly 300% speed increase!

The DS Structure

COMT uses the DS and PV structures that are available in the GAUSS Run-Time Library.

The DS structure is completely flexible, allowing you to pass anything you can think of into your procedure. There is a member of the structure for every GAUSS data type.

struct DS {
scalar type;
matrix dataMatrix;
array dataArray;
string dname;
string array vnames;
};

The PV Structure

The PV structure revolutionizes how you pass the parameters into the procedure. No longer do you have to struggle to get the parameter vector into matrices for calculating the function and its derivatives, trying to remember, or figure out, which parameter is where in the vector.

If your log-likelihood uses matrices or arrays,you can store them directly into the PV structure and remove them as matrices or arrays with the parameters already plugged into them. The PV structure can handle matrices and arrays in which some of their elements are fixed and some free. It remembers the fixed parameters and knows where to plug in the current values of the free parameters. It can also handle symmetric matrices in which parameters below the diagonal are repeated above the diagonal.

b0 – Mean paramters.
garch – GARCH parameters.
arch – ARCH parameters.
omega – Constant in variance equation.

There is no longer any need to use global variables. Anything the procedure needs can be passed into it through the DS structure. And these new applications uses control structures rather than global variables. This means, in addition to thread safety, that it is straightforward to nest calls to COMT inside of a call to COMT, QNewtonmt, QProgmt, or EQsolvemt.

Example:

A Markowitz mean/variance portfolio allocation analysis on a thousand or more securities would be an example of a large scale problem CO could handle.

CO also contains a special technique for semi-definite problems, and thus it will solve the Markowitz portfolio allocation problem for a thousand stocks even when the covariance matrix is computed on fewer observations than there are securities.

Because CO handles general nonlinear functions and constraints, it can solve a more general problem than the Markowitz problem. The efficient frontier is essentially a quadratic programming problem where the Markowitz Mean/Variance portfolio allocation model is solved for a range of expected portfolio returns which are then plotted against the portfolio risk measured as the standard deviation:



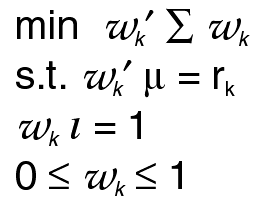
where l is a conformable vector of ones, and where 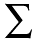is the observed covariance matrix of the returns of a portfolio of securities, and µ are their observed means.

This model is solved for



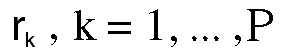
and the efficient frontier is the plot of r_k on the vertical axis against



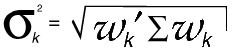
on the horizontal axis. The portfolio weights in W_k describe the optimum distribution of portfolio resources across the securities given the amount of risk to return one considers reasonable.

Because of CO's ability to handle nonlinear constraints, more elaborate models may be considered. For example, this model frequently concentrates the allocation into a minority of the securities. To spread out the allocation one could solve the problem subject to a maximum variance for the weights, i.e., subject to



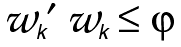
where 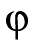 is a constant setting a ceiling on the sums of squares of the weights.

correlation matrix



This data was taken from from Harry S. Marmer and F.K. Louis Ng, "Mean-Semivariance Analysis of Option-Based Strategies: A Total Asset Mix Perspective", Financial Analysts Journal, May-June 1993.

An unconstrained analysis produced the results below:



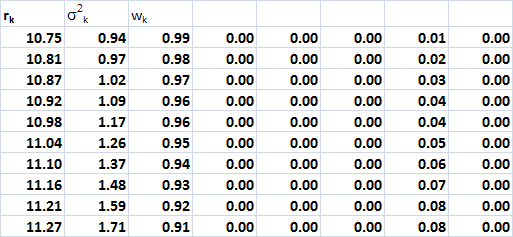
It can be observed that the optimal portfolio weights are highly concentrated in T-bills.

Now let us constrain w´w to be less than, say, .8. We then get:



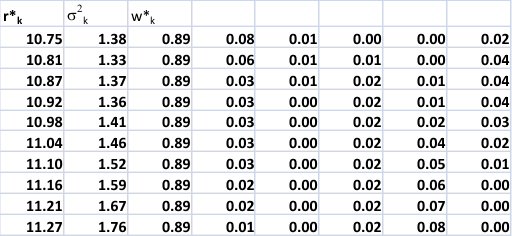
The constraint does indeed spread out the weights across the categories, in particular stocks seem to receive more emphasis.



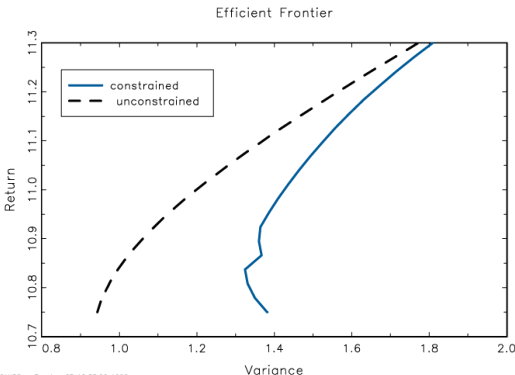Efficient portfolio for these analyses

We see there that the constrained portfolio is riskier everywhere than the unconstrained portfolio given a particular portfolio return.

In summary, CO is well-suited for a variety of financial applications from the ordinary to the highly sophisticated, and the speed of GAUSS makes large and time-consuming problems feasible.

CO is an advanced GAUSS Application and comes as GAUSS source code.

GAUSS Applications are modules written in GAUSS for performing specific modeling and analysis tasks. They are designed to minimize or eliminate the need for user programming while maintaining flexibility for non-standard problems.

The primary descent method for the single dependent variable is the classical Levenberg-Marquardt method. This method takes advantage of the structure of the nonlinear least squares problem, providing a robust and swift means for convergence to the minimum. If, however, the model contains a large number of coefficients to be estimated, this method can be burdensome because of the requirement for storing and computing the information matrix. For such models the Polak-Ribiere version of the conjugate gradient method is provided, which does not require the storage or computation of this matrix.