| |
GAUSS Applications
Pre-written, customizable
GAUSS programs designed to
increase user productivity and extend GAUSS
functionality in the fields
of statistics, finance, engineering, physics,
risk analysis and more.
Algorithmic
Derivatives
|
A program for
generating GAUSS procedures for
computing algorithmic derivatives.
|
Constrained
Maximum Likelihood MT
|
Constrained Maximum
Likelihood MT provides for the
estimation of statistical models by
maximum likelihood while allowing
for the imposition of general
constraints on the parameters, linear or
nonlinear, equality or inequality, as
well as bounds.
|
| Constrained
Optimization MT |
Basic sample statistics
including means, frequencies and
crosstabs. |
| Constrained
Optimization |
Solves the nonlinear
programming problem subject to general
constraints on the parameters. |
CurveFit
|
Nonlinear curve fitting.
|
Descriptive Statistics MT
|
Basic sample statistics
including means, frequencies
and crosstabs. This application is
thread-safe and takes advantage of
structures.
|
| Discrete
Choice |
A statistical package for
estimating discrete choice
and other models in which the dependent
variable is qualitative in some
way.
|
|
FANPAC MT |
Comprehensive suite of
GARCH (Generalized AutoRegressive
Conditional Heteroskedastic) models for
estimating volatility.
|
Linear
Programming MT
|
Solves small and large
scale linear programming problems
|
Linear
Regression MT
|
Least squares estimation.
|
Loglinear
Analysis MT
|
Analysis of categorical
data using loglinear analysis.
|
Maximum
Likelihood MT
|
Maximum likelihood
estimation of the parameters of
statistical models; uses structures,
allowing calls to be safely nested
or called in threaded programs, and some
calculations are themselves
threaded.
|
Maximum Likelihood
|
Maximum
likelihood estimation of the parameters
of statistical models.
|
Nonlinear Equations MT
|
Solves
systems of nonlinear equations having as
many equations as unknowns.
|
Optimization MT
|
Unconstrained
optimization;
uses structures, allowing calls to be
safely nested or
called in threaded programs, and some
calculations are themselves
threaded.
|
Optimization
|
Unconstrained
optimization.
|
Time Series MT
|
Exact ML
estimation
of VARMAX, VARMA, ARIMAX, ARIMA, and ECM
models subject to general
constraints on the parameters. Panel
data estimation. Unit root and
cointegration tests.
|
Algorithmic Derivatives
The
GAUSS AD 1.0 module is an application program
for generating GAUSS
procedures for computing algorithmic
derivatives. A major achievement
of AD is improved accuracy for optimization.
Numerical derivatives
invariably produce a loss of precision. The
loss of precision is
greater for standard errors than it is for
estimates.
At the default tolerance, Constrained Maximum
Likelihood (CML) and
Maximum Likelihood (Maxlik) can be expected
generally to have four or
five places of accuracy, whereas standard
errors will have about two
places. Accuracy essentially doubles with AD.
AD works independently of
any application to improve derivatives, and it
can be used with any
application that uses derivatives.
For some types of optimization problems,
convergence is accelerated.
Iterations are faster and fewer of them are
needed to achieve
convergence. The types of problems that will
see the most improvement
are those with a large amount of computation.
Constrained Maximum Likelihood 2.0.6+ and
Maximum Likelihood 5.0.7+ have been updated to
improve speed with AD.
Available for Windows, LINUX, and Mac.
Requires GAUSS Mathematical and Statistical
System 6.0 or the GAUSS Engine 6.0.
Constrained Mamximum Lkelihood MT (CMLMT) i
Features
- Parameter Estimation
- Statistical Inference – Wald, Bootstrap,
Confidence Limits by Inversion
- Heteroskedastic-consistent Covariance
Matrix of Parameters
- Profile Likelihood
- Weighted Maximum Likelihood
- BFGS, DFP, Newton, BHHH descent
algorithms
- Stepbt, Brent, Half Step, Augmented
Penalty, BHHH step, Wolfe’s Line Search
Methods
- Numerical Gradient, Hessian
Provide a GAUSS procedure for computing the
log-likelihood of your statistical model, and Constrained Maximum
Likelihood MT
does the rest. Using an iterative
Sequential Quadratic
Programming method parameter estimates along
with standard errors and
confidence limits are generated.
Example
Suppose we have a dependent variable that is
observed in several
ordered categories. We might estimate
coefficients of a
regression on this variable using the ordered
probit model:
where
and
Assuming  we have we have

where where is
the Normal cumulative distribution function. where is
the Normal cumulative distribution function.
The log-likelihood function for this model is
The cmlmt
function that
performs the estimation takes four arguments,
(1) a pointer to the
procedure that computes the log-likelihood, (2)
a PV parameter
structure containing the start values of the
parameters, (3) a DS data
structure, and (4) a control structure.
GAUSS structures are simply bins containing
other objects such as
matrices, strings, arrays, etc. They can
be defined by the
programmer, but the two of the structures used
by cmlmt are defined in
the Run-Time Library, and the control structure
is defined in the cmlmt
library.
The PV
Parameter Structure
The
PV parameter structure is created and filled
using GAUSS Run-Time
Library functions. Using these functions
the structure can be
filled with vectors, matrices, and arrays
containing starting parameter
values. Masks can be used to specify fixed
versus free
parameters. For example,
struct PV p0;
// creates a default parameter structure
p0 = pvCreate;
p0 = pvPack(p0,.5|.5|.5,”beta”);
p0 = pvPackm(p0,-30|-1|1|30,”tau”,0|1|1|0);
The structure now contains starting values for a
3×1
vector of coefficients called beta,and another
4×1 vector of thresholds
called tau. It will be convenient for the
calculation of the
log-likelihood for the first and last be
parameters set to -30 and
+30. The fourth argument is a mask
specifying the first and last
elements of the vector to be fixed and the
remaining elements free
parameters to be estimated.
The DS
Data Structure
The
DS data structure is a general purpose
bucket of GAUSS types. It
contains one of each of the types, matrix,
array, string, string array,
sparse matrix, and scalar. It is
passed to the log-likelihood
procedure untouched by cmlmt. It can
be used by programmers in
any way they choose to help in computing the
log-likelihood.
Typically it is used to pass data to the
procedure. The DS
structure can also be reshaped into a vector
of structures giving the
programmer great flexibility in handling
data and other information.
load x[200,5] = data.csv;
struct DS d0;
// creates a 2x1 vector of
// default data structures
d0 = reshape(dsCreate,2,1);
// dependent variable
d0[1].dataMatrix = x[.,1];
// independent variables
d0[2].dataMatrix = x[.,2:4];
The cmlmtControl
Structure
This structure handles the matrices and
strings that
control the estimation process such as
setting the descent algorithm,
the line search method, and so on. It
is also used to specify the
constraints. For example the
thresholds need to be constrained in
the following way where . This implies
the two free constraints
The programmer will accomplish by specifing
two members of the
cmlmtControl structure, C and D, to impose
this inequality constraint
where x is the vector of parameters being
estimated. Then
struct cmlmtControl c0;
// creates a default structure
c0 = cmlmtControlCreate;
c0.C = { 0 0 0 -1 1
0,
0 0 0 0 -1 1 };
c0.D = { 0,
0 };
The first three columns of the matrix c0.C
and the vector c0.D are
associated with regression coefficients that
are unconstrained and the
last two are associated with the thresholds.
The Log-likelihood Procedure
The programmer now writes a GAUSS procedure
computing a vector of
log-likelihood probabilities. This
procedure has three input
arguments, the PV parameter structure, the
DS data structure, and 3×1
vector the first element of which is nonzero
if cmlmt is requesting the
vector of log-likelihood probabilities, the
second element nonzero if
it is requesting the matrix of first
derivatives with respect to the
parameters, and the third element nonzero if
it is requesting the
Hessian or array of second derivatives with
respect to the
parameters. It has one return
argument, a modelResults structure
containing the results.
proc orderedProbit(struct PV p, struct DS d,
ind);
local mu, tau, beta, emu, eml;
struct modelResults mm;
if ind[1] == 1;
tau =
pvUnpack(p,”tau”);
beta =
pvUnpack(p,”beta”);
mu =
d[2].dataMatrix * beta;
eml =
submat(tau,d[1].dataMatrix,0) – mu;
emu =
submat(tau,d[1].dataMatrix + 1,0) – mu;
mm.function =
ln(cdfn(emu) – cdfn(eml));
endif;
retp(mm);
endp;
The GAUSS submat function serves to pull out
the k-th element of tau for the i-th row of
d[1].datamatrix set to k.
Since this procedure doesn’t return a matrix
of first derivatives nor
an array of second derivatives they will be
computed numerically by
cmlmt.
The result stored in mm.function is an Nx1
vector of log-probabilities
computed by observation. If we were to
have provided analytical
derivatives, the first derivatives would be
an Nxm matrix of
derivatives computed by observation where m
is the number of parameters
to be estimated, and the second derivatives
would be an Nxmxm array of
second derivatives computed by
observation. Computing these
quantities in this way improves
accuracy. It also allows for the
BHHH descent method which is more accurate
than other methods
permitting a larger convergence tolerance.
It is also possible to return a scalar
log-likelihood which is the sum
of the individual log-probabilities.
In this case the analytical
first derivatives would be a 1xm gradient
vector, and the second
derivatives a 1xmxm array. You would
also need to set c0.numObs
to the number of observations since cmlmt is
no longer able to
determine the number of observations from
the length of the vector of
log-probabilities.
The Command File
Finally we put it all together in the
command file:
library cmlmt;
// contains the structure definitions
#include cmlmt.sdf;
// simulating data here
x = rndn(200,3);
b = { .4, .5, .6 };
ystar = x*b;
tau = { -50, -1, 0, 1, 50 };
y = (ystar .> tau[1] .and ystar .<=
tau[2]) +
2 * (ystar .> tau[2] .and
ystar .<= tau[3]) +
3 * (ystar .> tau[3] .and
ystar .<= tau[4]) +
4 * (ystar .> tau[4] .and
ystar .<= tau[5]);
struct DS d0;
// creates a 2x1 vector of
// default data structures
d0 = reshape(dsCreate,2,1);
// dependent variable
d0[1].dataMatrix = y;
// independent variables
d0[2].dataMatrix = x;
struct PV p0;
// creates a default parameter structure
p0 = pvCreate;
p0 = pvPack(p0,.5|.5|.5,"beta");
p0 =
pvPackm(p0,-30|-1|0|1|30,"tau",0|1|1|1|0);
struct cmlmtControl c0;
// creates a default structure
c0 = cmlmtControlCreate;
c0.C = { 0 0 0 -1 1
0,
0 0 0 0 -1 1 };
c0.D = { 0,
0};
struct cmlmtResults out;
out = cmlmt(&orderedProbit,p0,d0,c0);
// prints the results
call cmlmtprt(out);
proc orderedProbit(struct PV p, struct DS d,
ind);
local mu, tau, beta, emu, eml;
struct modelResults mm;
if ind[1] == 1;
tau =
pvUnpack(p,"tau");
beta =
pvUnpack(p,"beta");
mu =
d[2].dataMatrix * beta;
eml =
submat(tau,d[1].dataMatrix,0) - mu;
emu =
submat(tau,d[1].dataMatrix + 1,0) - mu;
mm.function =
ln(cdfn(emu) - cdfn(eml));
endif;
retp(mm);
endp;
This program produces the following output:
================================================================
CMLMT Version
2.0.7
3/30/2012 1:29 pm
=================================================================
return code = 0
normal convergence
Log-likelihood
-15.1549
Number of cases 200
Covariance of the parameters computed by the
following method:
ML covariance matrix
Parameters
Estimates Std.
err. Est./s.e.
Prob. Gradient
------------------------------------------------------------------
beta[1,1]
4.2060
0.2385
17.634
0.0000 0.0000
beta[2,1]
5.3543
0.2947
18.166
0.0000 0.0000
beta[3,1]
6.2839
0.2789
22.531
0.0000 0.0000
tau[2,1]
-10.7561
0.7437
-14.462
0.0000 0.0000
tau[3,1]
-0.0913
0.2499
-0.365
0.7148 0.0000
tau[4,1]
10.6693
0.5697
18.727
0.0000 0.0000
Correlation matrix of the parameters
1
0.52064502
0.54690534
-0.46731768
0.046211496 0.57202935
0.52064502
1
0.58363048
-0.47574225
-0.061765839 0.65959766
0.54690534
0.58363048
1
-0.5169026
-0.0059238287 0.69077806
-0.46731768
-0.47574225
-0.5169026
1
0.0046253798 -0.44858539
0.046211496 -0.061765839
-0.0059238287
0.0046253798 1
-0.01457591
0.57202935
0.65959766
0.69077806
-0.44858539
-0.01457591 1
Wald Confidence Limits
0.95 confidence limits
Parameters
Estimates Lower
Limit Upper Limit
Gradient
----------------------------------------------------------------------
beta[1,1]
4.2060
3.7355
4.6764
0.0000
beta[2,1]
5.3543
4.7730
5.9356
0.0000
beta[3,1]
6.2839
5.7338
6.8339
0.0000
tau[2,1]
-10.7561
-12.2230
-9.2893
0.0000
tau[3,1]
-0.0913
-0.5842
0.4015
0.0000
tau[4,1]
10.6693
9.5457
11.7929
0.0000
Number of iterations 135
Minutes to
convergence 0.00395
Constrained Optimization MT (COMT)
solves the Nonlinear Programming problem,
subject to general
constraints on the parameters – linear or
nonlinear, equality or
inequality, using the Sequential Quadratic
Programming method in
combination with several descent methods
selectable by the user:
- Newton-Raphson
- quasi-Newton (BFGS and DFP)
- Scaled quasi-Newton
There
are also several selectable line search
methods. A Trust Region method
is also available which prevents saddle
point solutions. Gradients can
be user-provided or numerically calculated.
COMT is fast and can handle
large, time-consuming problems because it
takes advantage of the speed
and number-crunching capabilities of GAUSS.
It is thus ideal for large
scale Monte Carlo or bootstrap simulations.
New
Features
- Internally threaded functions
- Uses structures
- Improved algorithm
- Allows for computing a subset of the
derivatives
analytically, and for combining the
calculation of the function and
derivatives, thus reducing calculations
in common between function and
derivatives
Threading
in COMT
If you have a multi-core processor you may
take advantage of COMT’s
internally threaded functions. An important
advantage of threading
occurs in computing numerical derivatives.
If the derivatives are
computed numerically, threading will
significantly decrease the time of
computation.
Example
We
ran a time trial of a covariance-structure
model on a quad-core
machine. As is the case for most real world
problems, not all sections
of the code are able to be run in parallel.
Therefore, the theoretical
limit for speed increase is much less than
(single-threaded execution
time)/(number of cores).
Even so, the execution time of our program
was cut dramatically:
Single-threaded execution time: 35.42
minutes
Multi-threaded execution time: 11.79 minutes
That is a nearly 300% speed increase!
The DS
Structure
COMT uses the DS and PV structures that
are available in the GAUSS Run-Time
Library.
The DS structure is completely
flexible, allowing
you to pass anything you can think of into
your procedure. There is a
member of the structure for every GAUSS data
type.
struct DS {
scalar type;
matrix dataMatrix;
array dataArray;
string dname;
string array vnames;
};
The PV
Structure
The PV structure revolutionizes how
you pass the
parameters into the procedure. No longer do
you have to struggle to get
the parameter vector into matrices for
calculating the function and its
derivatives, trying to remember, or figure
out, which parameter is
where in the vector.
If your log-likelihood uses matrices or
arrays,you can store them
directly into the PV structure and remove
them as matrices or arrays
with the parameters already plugged into
them. The PV structure can
handle matrices and arrays in which some of
their elements are fixed
and some free. It remembers the fixed
parameters and knows where to
plug in the current values of the free
parameters. It can also handle
symmetric matrices in which parameters below
the diagonal are repeated
above the diagonal.
b0 – Mean paramters.
garch – GARCH parameters.
arch – ARCH parameters.
omega – Constant in variance equation.
There is no longer any need to use global
variables. Anything the
procedure needs can be passed into it
through the DS structure. And
these new applications uses control
structures rather than global
variables. This means, in addition to thread
safety, that it is
straightforward to nest calls to COMT inside
of a call to COMT,
QNewtonmt, QProgmt, or EQsolvemt.
Available for Windows, Mac,
Linux and Solaris. Requires GAUSS/GAUSS
Light version 10 or higher.

Constrained Optimization (CO)
CO is an applications module
written in the GAUSS programming language.
It solves the Nonlinear Programming problem,
subject to general
constraints on the parameters - linear or
nonlinear, equality or
inequality, using the Sequential Quadratic
Programming method in
combination with several descent methods
selectable by the user -
Newton-Raphson, quasi-Newton (BFGS and DFP), and
scaled quasi-Newton.
There are also several selectable line search
methods. A Trust Region
method is also available which prevents saddle
point solutions.
Gradients can be user-provided or numerically
calculated.
CO is fast and can handle large, time-consuming
problems because it
takes advantage of the speed and
number-crunching capabilities of
GAUSS. It is thus ideal for large scale Monte
Carlo or bootstrap
simulations.
Example
A Markowitz mean/variance portfolio allocation
analysis on a thousand
or more securities would be an example of a
large scale problem CO
could handle.
CO also contains a special technique for
semi-definite problems, and
thus it will solve the Markowitz portfolio
allocation problem for a
thousand stocks even when the covariance matrix
is computed on fewer
observations than there are securities.
Because CO handles general nonlinear functions
and constraints, it can
solve a more general problem than the Markowitz
problem. The efficient
frontier is essentially a quadratic programming
problem where the
Markowitz Mean/Variance portfolio allocation
model is solved for a
range of expected portfolio returns which are
then plotted against the
portfolio risk measured as the standard
deviation:
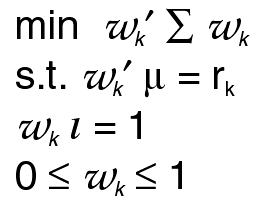
where l is a conformable vector of ones, and
where 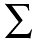 is the observed
covariance matrix of the returns of a portfolio
of securities, and µ are their observed means. is the observed
covariance matrix of the returns of a portfolio
of securities, and µ are their observed means.
This model is solved for
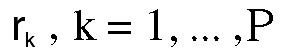
and the efficient frontier is the plot of rk
on the vertical axis against
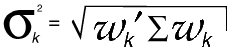
on the horizontal axis. The portfolio weights in
Wk describe
the optimum distribution of portfolio resources
across the securities
given the amount of risk to return one considers
reasonable.
Because of CO's ability to handle nonlinear
constraints, more elaborate
models may be considered. For example, this
model frequently
concentrates the allocation into a minority of
the securities. To
spread out the allocation one could solve the
problem subject to a
maximum variance for the weights, i.e., subject
to
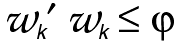
where  is a
constant setting a ceiling on the sums of
squares of the weights. is a
constant setting a ceiling on the sums of
squares of the weights.
correlation matrix

This data was taken from from Harry S. Marmer
and F.K. Louis Ng,
"Mean-Semivariance Analysis of Option-Based
Strategies: A Total Asset
Mix Perspective", Financial Analysts Journal,
May-June 1993.
An unconstrained analysis produced the results
below:
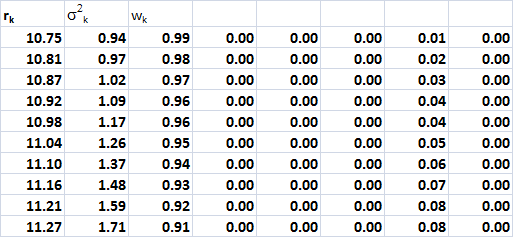
It can be observed that the optimal portfolio
weights are highly concentrated in T-bills.
Now let us constrain w´w to be less than, say,
.8. We then get:
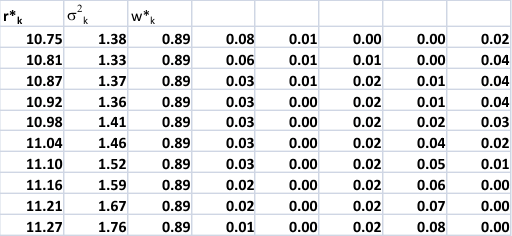
The constraint does indeed spread out the
weights across the categories, in particular
stocks seem to receive more emphasis.
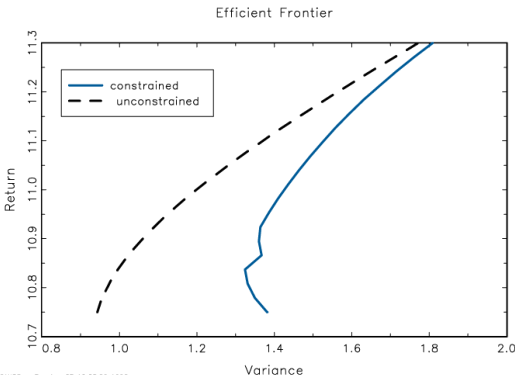
Efficient
portfolio for these analyses
We see there that the constrained
portfolio is
riskier everywhere than the unconstrained
portfolio given a particular
portfolio return.
In summary, CO is well-suited for a variety of
financial applications
from the ordinary to the highly sophisticated,
and the speed of GAUSS
makes large and time-consuming problems
feasible.
CO is an advanced GAUSS Application and comes as
GAUSS source code.
GAUSS Applications are modules written in GAUSS
for performing specific
modeling and analysis tasks. They are designed
to minimize or eliminate
the need for user programming while maintaining
flexibility for
non-standard problems.
Available for Windows, Mac, Linux and
Solaris. Requires GAUSS/GAUSS Light version
8.0 or higher.
CurveFit
Given data and a procedure for computing the
function, CurveFit will
find a best fit of the data to the function in
the least squares sense.
Special Features
- Weight observations
- Multiple dependent variables
- Bootstrap estimation
- Histogram and surface plots of
bootstrapped coefficients
- Profile t, and profile likelihood trace
plots
- Levenberg-Marquardt descent method
- Polak-Ribiere conjugate gradient descent
method
- Ability to activate and inactivate
coefficients
- Heteroskedastic-consistent covariance
matrix of coefficients
Bootstrap Estimation
CurveFit includes special
procedures for computing
bootstrapped estimates. One procedure produces
a mean vector and
covariance matrix of the bootstrapped
coefficients. Another generates
histogram plots of the distribution of the
coefficients and surface
plots of the parameters in pairs. The plots
are especially valuable for
nonlinear models because the distributions of
the coefficients may not
be unimodal or symmetric.
Profile t, and Profile Likelihood Trace
Plots
Also included in the module
is a procedure that
generates profile t trace plots and profile
likelihood trace plots
using methods described in Bates and Watts,
"Nonlinear Regression
Analysis and its Applications". Ordinary
statistical inference can be
very misleading in nonlinear models. These
plots are superior to usual
methods in assessing the statistical
significance of coefficients in
nonlinear models.
Descent Methods
The primary
descent
method for the single dependent variable is
the classical
Levenberg-Marquardt method. This method
takes advantage of the
structure of the nonlinear least squares
problem, providing a robust
and swift means for convergence to the
minimum. If, however, the model
contains a large number of coefficients to
be estimated, this method
can be burdensome because of the requirement
for storing and computing
the information matrix. For such models the
Polak-Ribiere version of
the conjugate gradient method is provided,
which does not require the
storage or computation of this matrix.
Multiple Dependent Variables
CurveFit allows multiple
dependent variables using a
criterion function permitting the
interpretation of the estimated
coefficients as either maximum likelihood
estimates or as Bayesian
estimates with a noninformative prior. This
feature is useful for
estimating the parameters of "compartment"
models, i.e., models arising
from linear first order differential
equations.
Available for Windows, Mac, Linux and
Solaris. Requires GAUSS/GAUSS Light version
8.0 or higher.

Descriptive
Statistics (MT 1.0)
The procedures in Descriptive
Statistics MT 1.0
provide basic statistics for the variables in
GAUSS data sets. These
statistics describe and test univariate and
multivariate features of
the data and provide information for further
analysis. Descriptive
Statistics MT 1.0 is a new product
that is thread-safe and takes advantage of
structures.
- Includes methods for analyzing and
generating contingency
tables and statistics for them.
- Includes new routines to compute
descriptive statistics,
including both univariate and multivariate
skew and kurtosis.
- Includes support for variable names of up
to 32 characters.
- Includes support for date variables where
applicable.
- You can now choose between two report
types-all variables
in a single table or individual reports for
each variable-and
you can choose which statistics to include
in the report and
the order in which they appear.
Descriptive Statistics MT 1.0 has methods for
analyzing and generating contingency tables and
producing statistics for them:
- Chi-Squared (Pearson and Likelihood Ratio)
- Phi
- Cramer's V
- Spearman s Rho
- Goodman-Krustal's Gamma Kendall's Tau-B
Stuart s Tau-C Somer's D
- Lamda
Descriptive Statistics MT 1.0 also has methods
for generating frequency
distributions with statistics, skew and
kurtosis, and tests for
differences of means.
Available for Windows, Mac, Linux and
Solaris. Requires GAUSS/GAUSS Light version
8.0 or higher.

Discrete
Choice is a package for the fitting
of a variety of models
with categorical dependent variables. These
models are particularly
useful for researchers in the social,
behavioral, and biomedical
sciences, as well as economics, public choice,
education, and marketing.
Output for these models includes full
information maximum likelihood
estimates with either standard and
quasi-maximum likelihood inference.
In addition, estimates of marginal effects are
computed either as
partials of the probabilities with respect to
the means of the
exogenous variables or optionally as the
average partials of the
probabilities with respect to the exogenous
variables.
Models
Nested logit
model
- Is derived from the assumption that
residuals have a
generalized extreme value distribution and
allows for a general pattern
of dependence among the responses thus
avoiding the IIA problem, i.e.,
the "independence of irrelevant
alternatives."
Conditional logit model
- Includes both variables that are
attributes of the
responses as well as, optionally, exogenous
variables that are
properties of cases.
Multinomial logit model
- Qualitative responses are each modeled
with a separate set of regression
coefficients
Adjacent category multinomial logit model
- The log-odds of one category versus the
next higher category is linear in the
cutpoints and explanatory variables
Stereotype multinomial logit model
- The coefficients of the regression in each
category are linear functions of a reference
regression
Poisson regression, left or right truncated,
left or right censored, or zero-inflated
models
- Estimates model with Poisson distributed
dependent
variable. This includes censored models -
the dependent variable is not
observed but independent variables are
available - and truncated models
where not even the independent variables are
observed. Also, a
zero-inflated Poisson model can be estimated
where the probability of
the zero category is a mixture of a Poisson
consistent probability and
an excess probability. The mixture
coefficient can be a function of
independent variables.
Negative binomial regression, left or right
truncated, left or right censored, or
zero-inflated models
- Estimates model with negative binomial
distributed
dependent variable. This includes censored
models - the dependent
variable is not observed but independent
variables are available - and
truncated models where not even the
independent variables are observed.
Also, a zero-inflated negative binomial
model can be estimated where
the probability of the zero category is a
mixture of a negative
binomial consistent probability and an
excess probability. The mixture
coefficient can be a function of independent
variables.
Logit, probit models
- Estimates dichotomous dependent variable
with either Normal or extreme value
distributions
Ordered logit, probit models
- Estimates model with an ordered
qualitative dependent variable with Normal
or extreme value distributions
Available
for Windows, Mac, Linux and Solaris.
Requires GAUSS/GAUSS Light version 8.0 or
higher.
FANPAC MT 3.0
FANPAC
MT is a set of threadsafe keyword commands and
procedures for the
econometric analysis of financial data. More
specifically, the
estimation of parameters of time series models
via the maximum
likelihood method. The package is divided into
two parts:
The package
is divided into two parts:
- Easy-to-program keyword commands which
simplify the modeling process
- GAUSS procedures, which can be called
directly to perform the computations,
allowing for great flexibility
New features
FANPAC MT 3.0 gives econometricians and
financial professionals access
to many new multivariate models, which provide a
better fit for some
financial problems. New models/features are
listed in orange.
 Available for Windows, Mac, Linux and
Solaris. Requires GAUSS/GAUSS Light version
8.0 or higher.
Available for Windows, Mac, Linux and
Solaris. Requires GAUSS/GAUSS Light version
8.0 or higher.
Linear Programming MT
Linear
Programming MT Module solves the standard
linear programming problem with the following
NEW and CUTTING-EDGE features:
- Thread-safe
Execution: Control
variables are model matrices are contained
in structures allowing
thread-safe execution of programs.
- Sparse
matrices: Linear Programming MT
exploits sparse matrix technology permitting
the analysis of problems
with very large constraint matrices. The
size of a problem that can be
analyzed is dependent on the speed and
amount of memory on the
computer, but problems with two to three
thousand constraints and more
than six thousand variables have been tested
on ordinary PC's.
- MPS files:
procedures are available for translating MPS
formatted files.
Other Product Features
LPMT is
designed to solve
small and large scale linear programming
problems. LPMT can be
initialized with a starting value, such as the
solution to a previous
problem which is similar to the one being
solved. This feature can
dramatically reduce the number of iterations
required to find a
feasible starting point.
Features
- Upper and lower finite bounds can be
provided for variables and constraints
- Problem type (minimization or
maximization)
- Constraint types (<=, >=, =)
- Choice of tolerances
- Pivoting rules
Computes
- The value of the variables and the
objective function upon termination, and
returns the dual variables
- State of each constraint
- Uniqueness and quality of solution
- Multiple optimal solutions if they exist
- Number of iterations required
- A final basis
- Can generate iterations log and/or final
report, if requested
Available for Windows, Mac, Linux and
Solaris. Requires GAUSS/GAUSS Light version
8.0 or higher.

Linear Regression MT
The Linear Regression MT
application module is a set
of procedures for estimating single equations
or a simultaneous system
of equations. It allows constraints on
coefficients, calculates het-con
standard errors, and includes two-stage least
squares, three-stage
least squares, and seemingly unrelated
regression. It is thread-safe
and takes advantage of structures found in
later versions of
GAUSS.
Features
- Calculates heteroskedastic-consistent
standard errors, and performs
both influence and collinearity diagnostics
inside the ordinary least
squares routine (OLS)
- All regression procedures can be run at a
specified data range
- Performs multiple linear hypothesis
testing with any form
- Estimates regressions with linear
restrictions
- Accommodates large data sets with
multiple variables
- Stores all important test statistics and
estimated coefficients in an efficient
manner
- Both three-stage least squares and
seemingly unrelated regression can be
estimated iteratively
- Thorough Documentation
- The comprehensive user's guide includes
both a
well-written tutorial and an informative
reference section. Additional
topics are included to enrich the usage of
the procedures. These
include:
- Joint confidence region for beta
estimates
- Tests for heteroskedasticity
- Tests of structural change
- Using ordinary least squares to estimate
a translog cost function
- Using seemingly unrelated regression to
estimate a system of cost share equations
- Using three-stage least squares to
estimate Klein's Model I
Available
for Windows, Mac, Linux and Solaris.
Requires GAUSS/GAUSS Light version 8.0 or
higher.

Loglinear Analysis MT
The Loglinear
Analysis MT
application module (LOGLIN) contains
procedures for the analysis of
categorical data using loglinear analysis.
This application is
thread-safe and takes advantage of structures.
The estimation is based on the assumption that
the cells of the K-way
table are independent Poisson random
variables. The parameters are
found by applying the Newton-Raphson method
using an algorithm found in
A. Agresti (1984) Analysis of Ordinal
Categorical Data.
You may construct your own design matrix or
use LOGLIN procedures to
compute one for you. You may also select the
type of constraint and the
parameters.
Features
- Fits a
hierarchical model given fit configurations
- Will fit all
3-way hierarchical models of a table
- Provides for
cell weights
- LOGLIN can
estimate most
of the models described in such texts as
Y.M.M. Bishop, S.E. Fienberg,
and P.W. Holland (1975) Discrete
Multivariate Analysis, S. Haberman
(1979) Analysis of Qualitative Data, Vols. 1
and 2, as well as the book
by A. Agresti.
Available for Windows, Mac, Linux and
Solaris. Requires GAUSS/GAUSS Light version
8.0 or higher.

Maximum Likelihood (MaxlikMT) MT 2.0
MaxlikMT 2.0 contains a set
of procedures for the solution of the maximum
likelihood problem with bounds on parameters.
Major
Features of MaxLikMT
- Structures
- Simple bounds
- Hypothesis testing for models with bounded
parameters
- Log-likelihood function
- AlgorithmSecant algorithms
- Line search methods
- Weighted maximum likelihood
- Active and inactive parameters
- Bounds
In MaxlikMT,
the same
procedure computing the log-likelihood or
objective function will be
used to compute analytical derivatives as well
if they are being
provided. Its return argument is a
maxlikmtResults structure with three
members, a scalar, or Nx1 vector containing
the log-likelihood (or
objective), a 1xK vector, or NxK matrix of
first derivatives, and a KxK
matrix or NxKxK array of second derivatives
(it needs to be an array if
the log-likelihood is weighted).
Of course the derivatives are optional, or
even partially optional,
i.e., you can compute a subset of the
derivatives if you like and the
remaining will be computed numerically. This
procedure will have an
additional argument which tells the function
which to compute, the
log-likelihood or objective, the first
derivatives, or the second
derivatives, or all three. This means that
calculations in common will
not have to be redone.
Available for
Windows, Mac, Linux
and Solaris. Requires GAUSS/GAUSS Light
version 10 or higher; Linux
requires version 10.0.4 or higher.

Maximum
Likelihood (MAXLIK)
MAXLIK
performs maximum
likelihood estimation of the parameters of
statistical models. All you
provide is a GAUSS function to calculate the
log-likelihood for a set
of observations. MAXLIK does the rest.
Major Features
of Maximum Likelihood
- More than 25
user-selectable options control the
optimization
- Fast
Procedures: FASTMAX, FASTBoot, FASTBayes,
FASTProfile, and FASTPflCLimits
can speed convergence times up to 800
percent over earlier versions of MAXLIK,
depending on the type of problem.
- "Kiss-Monster"
random numbers used in the bootstrap
procedure and random line search algorithm.
- The bootstrap
and random line search procedures use
the new "Kiss-Monster" random number
generator. It has a period of
10^8859, long enough for serious Monte Carlo
work.
- Descent
algorithms include: BFGS
(Broyden-Fletcher-Goldfarb-Shanno), DFP
(Davidon-Fletcher-Powell),
Newton, steepest descent, PRCG
(Polak-Ribiere-type conjugate gradient),
and BHHH (Berndt-Hall-Hall-Hausman)
- Step-length
methods include: STEPBT, BRENT, BHHHSTEP,
and a step-halving method
- A "switching"
method may also be selected which
switches the algorithm during the iterations
according to three
criteria: number of iterations, failure of
the function to decrease
within a tolerance, or decrease of the line
search step length below a
tolerance
Improved
Algorithm
MAXLIK
implements the
Cholesky factorization, solve, and update
methods for the BFGS, DFP,
and Newton algorithms. Event Count and
Duration Regression
An included COUNT module (by Gary King,
Harvard University) estimates
limited dependent variable models. These
procedures provide maximum
likelihood estimator s for parametric
regression models of events data,
i.e., models with dependent variables that are
measured either as event
counts or as durations between events.
Available
for Windows, Mac, Linux and Solaris.
Requires GAUSS/GAUSS Light version 8.0 or
higher.
Nonlinear Equations MT
The Nonlinear
Equations
MT applications module (NLSYS) solves systems
of nonlinear equations
where there are as many equations as unknowns.
This application is
thread-safe and takes advantage of structures
found in later versions
of GAUSS.
The functions must be continuous and
differentiable. You may provide a
function for calculating the Jacobian, if
desired. Otherwise NLSYS will
compute the Jacobian numerically. You can also
select from two descent
algorithms, the Newton method or the secant
update method, and from two
step-length methods, a quadratic/cubic method,
or the hookstep method.
Available for Windows, Mac, Linux and
Solaris. Requires GAUSS/GAUSS Light version
8.0 or higher.

Optimization MT (OPMT) 1.0
OPMT is intended for the
optimization of functions.
It has many features, including a wide
selection of descent algorithms,
step-length methods, and "on-the-fly"
algorithm switching. Default
selections permit you to use Optimization with
a minimum of programming
effort. All you provide is the function to be
optimized and start
values, and OPMT does the rest.
Special Features in Optimization MT 1.0
-
Internally threaded.
-
Uses structures.
-
Allows for placing bounds on the
parameters.
-
Allows for computing a subset of the
derivatives
analytically, and for combining the
calculation of the function and
derivatives, thus reducing calculations in
common between function and
derivatives.
- More than 25 options can be easily
specified by the user to control the
optimization
- Descent algorithms include: BFGS, DFP,
Newton, steepest descent, and PRCG
- Step length methods include: STEPBT,
BRENT, and a step-halving method
- A "switching" method may also be selected
which
switches the algorithm during the iterations
according to two criteria:
number of iterations, or failure of the
function to decrease within a
tolerance
Available for Windows, Mac, Linux and
Solaris. Requires GAUSS/GAUSS Light version
10 or higher.

Optimization
Optimization
is intended
for the optimization of functions. It has many
features, including a
wide selection of descent algorithms,
step-length methods, and
"on-the-fly" algorithm switching. Default
selections permit you to use
Optimization with a minimum of programming
effort. All you provide is
the function to be optimized and start values,
and Optimization does
the rest.
Features
- More than 25 options can be easily
specified by the user to control the
optimization
- Descent algorithms include: BFGS, DFP,
Newton, steepest descent, and PRCG
- Step length methods include: STEPBT,
BRENT, and a step-halving method
- A "switching" method may also be selected
which
switches the algorithm during the iterations
according to two criteria:
number of iterations, or failure of the
function to decrease within a
tolerance
Improved
Algorithm
Optimization
implements
the numerically superior Cholesky
factorization, solve and update
methods for the BFGS, DFP, and Newton
algorithms. The Hessian, or its
estimate, are updated rather than the inverse
of the Hessian, and the
descent is computed using a solve. This
results in better accuracy and
improved convergence over previous methods.
Available for Windows, Mac, Linux and
Solaris. Requires GAUSS/GAUSS Light version
8.0 or higher.

Time Series MT 1.0
Time Series MT
1.0 is the newest time
series application available for GAUSS. This
new product will
streamline the creation of large GAUSS
programs that utilize Time
Series models.
Features
-
LSDV - Least Squares
Dummy Variable model for multivariate data
with bias correction of the parameters
-
Switch - Hamilton's
Regime-Switching Regression model
-
SVARMAX - Seasonal VARMAX model:
SVARMAX(p,d,q,P,D,Q)s
- TSCS - Time Series Cross-Sectional
Regression models
Autoregressive Models
- Computes estimates of the parameters and
standard errors for a regression model with
autoregressive errors.
Matrices
- Portmanteau Statistics
- Forecasting: Univariate and Multivariate
- Univariate Simulation
Switching
Regression
- Bayesian prior
- Constraints on transition probabilities
Additional
Features
- Exact full information maximum likelihood
(FIML) estimation of VARMAX and VARMA,
ARIMAX, ARIMA, ECM models.
- Impose general linear and nonlinear and
equality
and inequality constraints on the
parameters. Find Lagrangean values
associated with each constraint. Return
ACF indicator matrices,
together with other summary information,
including Akaike, Schwarz, and
Bayesian information criteria. Compute
forecasts from VARMAX and VARMA
models.
- Exact maximum likelihood estimation of ECM
models.
- Unit root and cointegration tests, DF,
ADF, Phillips-Perron, and Johansen's Trace
and Maximum Eigenvalue tests.
- Estimation of VAR models.
- Compute parameter estimates and standard
errors for
a regression model with autoregressive
errors. Can be used for models
for which the Cochrane-Orcutt or similar
procedures are used. Also
computes autocovariances and
autocorrelations of the error term.
- ARIMA Models
- The Time Series module includes tools
for
estimating general ARIMA (p,d,q) models
using an exact MLE procedure
based on C. Ansley (Biometrika 1979, pp.
59-65). Procedures for
computing forecasts, theoretical
autocovariances, sample
autocorrelations, and partial
autocorrelations (using Durbin's
algorithm), as well as for simulating
ARIMA models are provided.
- Time-Series Cross-Sectional Regression
Models: TSCS
- This module provides procedures to
compute
estimates for "pooled time-series
cross-sectional" models. The
assumption is that there are multiple
observations over time on a set
of cross-sectional units (e.g., people,
firms, countries).
For example, the analyst may have data for
a cross-section of
individuals each measured over 10 time
periods. While these models were
devised to study a cross-section of units
over multiple time periods,
they also correspond to models in which
there are data for groups such
as schools or firms with measurements on
multiple observations within
the group (e.g., students, teachers,
employees).
The specific model that can be estimated
with this program is a
regression model with variable intercepts.
That is, a model with
individual-specific effects. The
regression parameters for the
exogenous variables are assumed to be
constant across cross-sectional
units. The intercept varies across
individuals. This program provides
three estimators:
- Fixed-effects OLS estimator (analysis
of covariance estimator)
- Constrained OLS estimator
- Random effects estimator using GLS
A
Hausman test is computed to show whether the
error components (random
effects)
model is the correct specification. In addition
to providing
the
analysis
of computed. The first partial squared
correlation shows the
percentage
of variation in the dependent variable that can
be explained
by
the
set of independent variables while holding
constant the group
variables.
The
second shows the extent to which variation in
the dependent
variable can
be
accounted for by the group variable after the
other independent
variables
have
been statistically held constant.
A key feature of this program is that it
allows for a variable number of
time-series
observations per cross-sectional unit. For
instance, there
might be 5
time-series observations for the first
individual, 10 for the
second, and so on. This is useful when there
are missing values.
Available for Windows, Mac, Linux and
Solaris. Requires GAUSS/GAUSS Light
version 8.0 or higher.
© Copyright 2004-2013
Aptech Systems, Inc.


|
|



