| |
Compute
Core Algorithms
With the world's largest collection of
algorithms in a single system, each able to operate across the widest
applicable scope of numeric, symbolic, or graphical input, Mathematica
provides broad coverage for mathematical computations and equation
solving in every field.
- Uniform expression model: Mathematica handles many
different kinds of concepts: mathematical formulas, lists, and
graphics, to name just a few. Although they often look very different,
Mathematica represents all of these in one uniform way—as expressions.
- Equation solving: Mathematica's numeric and symbolic
equation solving capabilities, all automatically selected through a
small number of powerful functions, include algebraic, differential,
recurrence, and functional equations and inequalities, as well as
linear systems.
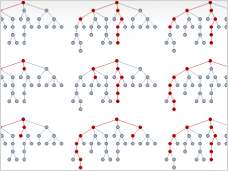 Graphs
and networks: Mathematica includes a large suite of fundamental graph
operations and algorithms, including finding paths, cycles, cliques,
and more. Create families of special graphs, generate random graphs, or
construct graphs interactively. Import and export to standard graph and
matrix formats. Graphs
and networks: Mathematica includes a large suite of fundamental graph
operations and algorithms, including finding paths, cycles, cliques,
and more. Create families of special graphs, generate random graphs, or
construct graphs interactively. Import and export to standard graph and
matrix formats.
- Linear algebra: Symbolic matrices, numerical matrices
of any precision, dense and sparse matrices, and matrices with millions
of entries: Mathematica handles them all, seamlessly switching among
large numbers of optimized algorithms.
- Discrete calculus: Mathematica delivers a
comprehensive system for discrete calculus, covering symbolic
operations, difference equations, generating functions, sequences, and
numerical discrete calculus.
- Polynomial algebra: Mathematica supports all aspects
of polynomial algebra, including factoring and decomposition,
structural operations, polynomial division, and more. Carefully tuned
strategies automatically select optimal algorithms, allowing
large-scale polynomial algebra.
 Number
theory: A complete library of functions covering multiplicative,
analytic, additive, and algebraic number theory, including factoring,
primes, congruences, and modular arithmetic, makes Mathematica the
ideal platform for number theoretic experiment, discovery, and proof. Number
theory: A complete library of functions covering multiplicative,
analytic, additive, and algebraic number theory, including factoring,
primes, congruences, and modular arithmetic, makes Mathematica the
ideal platform for number theoretic experiment, discovery, and proof.
- Mathematical constants and data: Built-in datasets of
finite groups, graphs, knots, lattices, polyhedra, and more are all
suitable for direct integration into calculations. Computations can
also use mathematical constants to any precision, and millions of
digits of constants like π and e can be calculated in seconds.
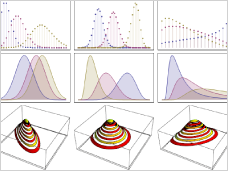 Probability
and statistics: Mathematica's broad coverage of statistics and data
analysis means more statistical distributions than any other system,
distributions that can be defined directly from data, support for
classical statistics, large-scale data analysis, statistical model
analysis, exploratory data analysis, symbolic manipulation and numeric
analysis, charting, and more. Probability
and statistics: Mathematica's broad coverage of statistics and data
analysis means more statistical distributions than any other system,
distributions that can be defined directly from data, support for
classical statistics, large-scale data analysis, statistical model
analysis, exploratory data analysis, symbolic manipulation and numeric
analysis, charting, and more.
- Calculus and analysis: Covering differentiation,
integration, series, Fourier analysis, integral transforms,
differential operators, and more, Mathematica's powerful capabilities
span the breadth of symbolic and numeric calculus.
 Computational
systems: Mathematica made possible Stephen Wolfram's exploration of the
computational universe and the emerging field of Wolfram Science (NKS).
Whether for modeling, algorithm discovery, or basic NKS, Mathematica
has immediate built-in capabilities for the systematic study of a broad
range of computational systems. Computational
systems: Mathematica made possible Stephen Wolfram's exploration of the
computational universe and the emerging field of Wolfram Science (NKS).
Whether for modeling, algorithm discovery, or basic NKS, Mathematica
has immediate built-in capabilities for the systematic study of a broad
range of computational systems.
- Logic and Boolean algebra: Incorporating
state-of-the-art quantifier elimination, satisfiability, and
equational-logic theorem proving, Mathematica provides a powerful
framework for investigations based on Boolean algebra.
- Special functions: Mathematica has the broadest and
deepest coverage of special functions, all of which support
arbitrary-precision evaluation for complex values of parameters;
arbitrary series expansion even at branch points; and an immense web of
exact relations, transformations, and simplifications.

Numerical Computing
Mathematica uses the power of symbolic computation
to make numerical computing faster and more accurate. Automatic
algorithm selection and the ability to use any calculation precision
enhance Mathematica's capabilities in linear algebra, quadrature, local
and global optimization, differential equation solving, and many more
areas.
- Task-oriented automatic solvers: Task-based
Mathematica functions solve problems by automatically selecting the
appropriate numerical method, even switching in mid-calculation. With
hundreds of methods to choose from, this optimized algorithm selection
improves speed and reliability over manual specification.
- Results at any precision: Any number precision or
number size can be used across all functions, allowing answers accurate
to almost any number of digits. Internally, higher-precision
calculations are often used automatically.

- Linear algebra and sparse arrays: Improve speed and
memory use with robust linear algebra on dense matrices using
industry-standard, high-performance libraries; sparse arrays of any
dimension; and numerical linear algebra on arbitrary precision and
mixed symbolic-numeric matrices.
 Integration
and summation: Compute single and multidimensional numerical integrals
and numerical sums and products of sequences. Many integration methods
including globally adaptive subdivision, Gaussian and Clenshaw-Curtis
quadrature rules, and specialized high-dimensional and oscillatory
rules. Integration
and summation: Compute single and multidimensional numerical integrals
and numerical sums and products of sequences. Many integration methods
including globally adaptive subdivision, Gaussian and Clenshaw-Curtis
quadrature rules, and specialized high-dimensional and oscillatory
rules.
- Numerical equation solving: Numerical root-finding of
functions and systems of simultaneous equations is built into
Mathematica. Methods include Newton, Secant, and Brent as well as
specialized methods for efficient numerical solutions of systems of
polynomial equations.
- Symbolically enhanced numeric computing: With
behind-the-scenes symbolic calculations, Mathematica optimizes
performance of numerical computations for time and accuracy—and makes
previously unsolvable calculations directly computable. Examples
include the intelligent handling of piecewise functions,
discontinuities, and automatic expression transformation ahead of
numerical sampling.
- Unique numerical precision tracking: Mathematica
automatically tracks and communicates how many digits of the result are
accurate, giving almost complete protection from numerical errors, be
they round-off errors or from badly conditioned systems.
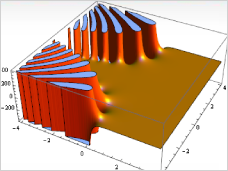
 Differential
equations: Numerically solve delay and differential-algebraic
equations, partial differential equations, and systems of nonlinear
differential equations of any order. Mathematica's built-in methods
include implicit and explicit Runge-Kutta and multistep methods,
specialized methods for stiff equations, method of lines, and many
more. Differential
equations: Numerically solve delay and differential-algebraic
equations, partial differential equations, and systems of nonlinear
differential equations of any order. Mathematica's built-in methods
include implicit and explicit Runge-Kutta and multistep methods,
specialized methods for stiff equations, method of lines, and many
more.
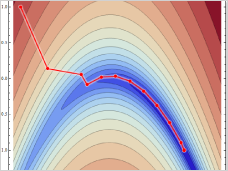 Local and global optimization: Mathematica includes a
full range of state-of-the-art optimization techniques, including
constrained and unconstrained local optimization using conjugate
gradient, interior point, and other methods; global optimization using
Nelder-Mead, simulated annealing, and oher methods; linear
programming; traveling salesman problems; and more. Local and global optimization: Mathematica includes a
full range of state-of-the-art optimization techniques, including
constrained and unconstrained local optimization using conjugate
gradient, interior point, and other methods; global optimization using
Nelder-Mead, simulated annealing, and oher methods; linear
programming; traveling salesman problems; and more.

Application Areas
In addition to being a comprehensive and
powerful computational system, Mathematica builds in specialized
functionality for many technical areas, from computational biology to
wavelet analysis. Every function is tightly integrated with the whole
Mathematica system, making it possible to investigate a single area in
great detail and explore new ideas at the intersection of different
fields.
- Statistics and data
analysis: From calculating basic descriptive statistics to developing
and visualizing multidimensional nonlinear models, Mathematica
streamlines the entire statistical analysis workflow. With hundreds of
distributions, automated parameter estimation, hypothesis testing,
statistical model analysis, and more, Mathematica provides a
comprehensive set of tools for assessing and understanding data.
- GPU programming:
Mathematica includes built-in support for CUDA and OpenCL environments,
making GPU programming broadly accessible for the first time. GPU
operations are fully integrated into the Mathematica system, including
direct exchange of data between processes and automatic compilation and
linking of GPU code.
- Control systems: Design and analyze control systems
using classical and state-space techniques, develop control solutions
for analog and digital systems, simulate models in open- and
closed-loop configurations, and interactively evaluate controllers—all
in one system.
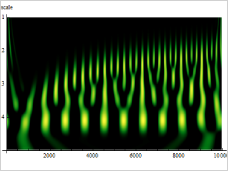 Wavelet
analysis: Mathematica brings a broad spectrum of wavelet analysis tools
to your desktop, including support for many wavelet families, and
continuous and discrete wavelet transforms. Wavelet transforms work
directly with arrays of any dimension as well as sound and image data,
providing a symbolic representation of the transform that can easily be
visualized or used for further processing. Wavelet
analysis: Mathematica brings a broad spectrum of wavelet analysis tools
to your desktop, including support for many wavelet families, and
continuous and discrete wavelet transforms. Wavelet transforms work
directly with arrays of any dimension as well as sound and image data,
providing a symbolic representation of the transform that can easily be
visualized or used for further processing.
 Parallel
computing: On any multicore computer, Mathematica automatically runs
multiple parts of a computation concurrently—making parallel computing
easy enough for everyday use. Mathematica's parallel infrastructure is
set up to allow seamless scaling to networks, clusters, grids, and
clouds, while the symbolic character of the Mathematica language
provides straightforward support of many programming paradigms and
data-sharing models. Parallel
computing: On any multicore computer, Mathematica automatically runs
multiple parts of a computation concurrently—making parallel computing
easy enough for everyday use. Mathematica's parallel infrastructure is
set up to allow seamless scaling to networks, clusters, grids, and
clouds, while the symbolic character of the Mathematica language
provides straightforward support of many programming paradigms and
data-sharing models.
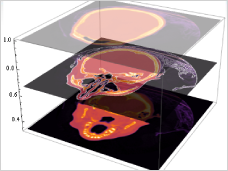 Image
processing and analysis: With dozens of features for real-time image
acquisition, filtering, segmentation, shape analysis, feature
detection, and more, Mathematica offers a complete environment and
interactive workflow for image processing and analysis. Image
processing and analysis: With dozens of features for real-time image
acquisition, filtering, segmentation, shape analysis, feature
detection, and more, Mathematica offers a complete environment and
interactive workflow for image processing and analysis.
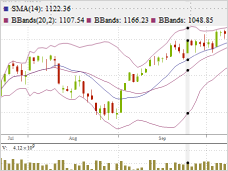 Financial
engineering: Mathematica includes built-in functions for pricing
derivatives, including exotic options; for computing bond values and
sensitivity measures; and for calculating time value of money. With
more than a hundred financial indicators, easy connectivity to
databases and web services, high-performance computing with built-in
parallel processing, and more, Mathematica has everything you need for
computational finance. Financial
engineering: Mathematica includes built-in functions for pricing
derivatives, including exotic options; for computing bond values and
sensitivity measures; and for calculating time value of money. With
more than a hundred financial indicators, easy connectivity to
databases and web services, high-performance computing with built-in
parallel processing, and more, Mathematica has everything you need for
computational finance.
- Geographical information
systems: With built-in geodesy data and comprehensive support for all
standard reference ellipsoids, datums, and projections, Mathematica
streamlines the process of importing, visualizing, and computing with
geospatial data from varied sources—allowing you to apply
high-precision geodetic techniques to your GIS applications.

Data Sources & Analysis
Mathematica can combine your imported
data with Wolfram|Alpha's computable data and immediately analyze it
using advanced model and data fitting, signal processing,
classification, or statistical methods. Highly customizable data
visualization features let you see your results in new ways.
- Hundreds of file formats: Process and analyze data
from diverse sources consistently using Mathematica's uniform symbolic
representation. Hundreds of file formats are supported for import and
export, including spreadsheets; XML; 2D and 3D graphics formats;
multimedia formats; document formats, including PDF and HTML;
compressed files; and many other data formats for specific application
areas.
 Database
connectivity: Mathematica connects to any standard SQL database, with
support for secure connections, result sets, connection pooling, and
transactions. It provides a high-level symbolic representation of
databases, queries, and results, as well as full support for
traditional string-based SQL queries. Database
connectivity: Mathematica connects to any standard SQL database, with
support for secure connections, result sets, connection pooling, and
transactions. It provides a high-level symbolic representation of
databases, queries, and results, as well as full support for
traditional string-based SQL queries.
- Statistical data analysis: With the largest set of
built-in distributions of any system, Mathematica offers a full suite
of statistical measures and operations, from mean and variance to
cumulants and information entropy. Advanced operations on data include
automatic hypothesis testing, distribution estimation, kernel density
estimation, and more.
 Data
visualization: Mathematica includes a full repertoire of functions for
visualizing structured and unstructured data in 2D and 3D. Built-in
functions include contour and density plots; point, line, and surface
plots; vector and streamline plots; histograms; and standard
statistical charts, such as pie, bar, bubble, and quantile charts. Data
visualization: Mathematica includes a full repertoire of functions for
visualizing structured and unstructured data in 2D and 3D. Built-in
functions include contour and density plots; point, line, and surface
plots; vector and streamline plots; histograms; and standard
statistical charts, such as pie, bar, bubble, and quantile charts.
- Cluster analysis: Mathematica's integrated
exploratory data analysis features include cluster detection, nearest
neighbor searching, a large library of standard distance and similarity
measures, data binning and histogram functions, and more.
 Direct
access to Wolfram|Alpha data: Instantly access Wolfram|Alpha's
continuously growing data collection. Compute with more than 10
trillion pieces of data in every field, including science, engineering,
finance, socioeconomics, and more. Access data programmatically, or
query in plain English. Direct
access to Wolfram|Alpha data: Instantly access Wolfram|Alpha's
continuously growing data collection. Compute with more than 10
trillion pieces of data in every field, including science, engineering,
finance, socioeconomics, and more. Access data programmatically, or
query in plain English.
- Language connectivity and web services: Mathematica
can natively call and be called by C, .NET, Java, and other languages;
automatically generate C code; compile standalone libraries or
executables; link to dynamic libraries at run time; and connect to WSDL
web services.
- Model fitting: Mathematica automates linear and
nonlinear model fitting, including logit and probit regression, and
provides full fit diagnostics such as confidence intervals, ANOVA
tables, and much more.
- Signal processing: Mathematica has complete support
for signal processing, with algorithms optimized to enable large
volumes of data. Features include linear and nonlinear filters, Fourier
and wavelet transforms, correlations and convolutions, fast linear
algebra, and interpolation and extrapolation.
- String analysis: Mathematica provides optimized
algorithms for substring detection, replacement, alignment, and pattern
matching using regular expressions and generalized symbolic patterns.

Graphics & Visualization
Functions, data,
diagrams, images, or annotations—Mathematica's visualization engine
powers high-quality static or dynamic representations, automatically
optimizing the balance between computational efficiency and visual
sophistication.
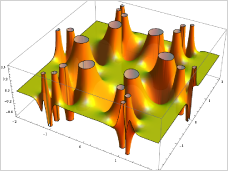 Function
visualization: With region- and volume-oriented implicit plotting,
automated singularity analysis, arbitrary plotting regions and mesh
overlays, and more, Mathematica enables the immediate creation of
highly aesthetic and technically correct 2D and 3D visualizations. A
comprehensive set of function visualization types are built in,
including polar and spherical plots, contour and density plots,
parametric line and surface plots, and vector and stream plots. Function
visualization: With region- and volume-oriented implicit plotting,
automated singularity analysis, arbitrary plotting regions and mesh
overlays, and more, Mathematica enables the immediate creation of
highly aesthetic and technically correct 2D and 3D visualizations. A
comprehensive set of function visualization types are built in,
including polar and spherical plots, contour and density plots,
parametric line and surface plots, and vector and stream plots.
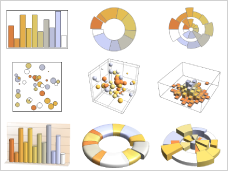 Business
charting: Mathematica allows you to immediately take data and produce
compelling dynamic visualizations of a wide variety of types including
histograms, 2D and 3D bar charts, pie charts, bubble charts, and more.
Options for advanced labeling and styling of individual chart elements
allow you to easily customize business graphics. Business
charting: Mathematica allows you to immediately take data and produce
compelling dynamic visualizations of a wide variety of types including
histograms, 2D and 3D bar charts, pie charts, bubble charts, and more.
Options for advanced labeling and styling of individual chart elements
allow you to easily customize business graphics.
- Symbolic graphics language: Mathematica's 2D and 3D
graphics are represented using symbolic primitives, and can therefore
be generated and manipulated using all standard Mathematica functions
and seamlessly integrated with text, math, or tables.
- Multimedia file formats: Mathematica natively
supports all standard raster, vector, and video formats, including GIF,
JPEG, PNG, SVG, EPS, AVI, FLV, QuickTime, SWF, and more. Import full
videos or individual video frames as images for immediate processing.
- Illustration and drawing tools: Built-in, interactive
graphics-editing tools in Mathematica make it easy to refine the
appearance of your visualizations or to create free-form ones from
scratch. The Mathematica Drawing Tools palette includes controls for
inserting and modifying standard graphics primitives and text,
specifying styles, and automating alignment and spacing.
- Data visualization: Visualize structured and
unstructured data in 2D and 3D with a wide variety of plotting
functions such as stream and vector plots, contour and density plots,
polar plots, and more. Easily plot curves and surfaces inferred from
point data; visualize the structure of arrays, including huge sparse
matrices; and more with Mathematica's built-in functions.
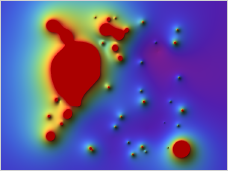 Field-specific
visualizations: Mathematica offers specialized visualizations for a
range of application areas such as finance, statistics, graph theory,
control systems, wavelets, and more. Create and work with candlestick
charts, quantile plots, box whisker charts, Bode plots, and many other
field-specific visualizations. Field-specific
visualizations: Mathematica offers specialized visualizations for a
range of application areas such as finance, statistics, graph theory,
control systems, wavelets, and more. Create and work with candlestick
charts, quantile plots, box whisker charts, Bode plots, and many other
field-specific visualizations.
- Visual styling and customization: Mathematica
provides hundreds of flexible options to control every aspect of your
visualizations, including plot size, axis labels, grid lines, meshes,
filling, 3D lighting, camera angle, and more—allowing you to generate
highly customized and professional-quality visualizations.
- Integrated image processing: Mathematica's built-in
image processing capabilities are fully integrated with its symbolic
graphics language, so it is easy to compose raster images and symbolic
graphics together. Apply operations such as segmentation, shape
analysis, feature detection, and filtering to raster images or any
graphics.
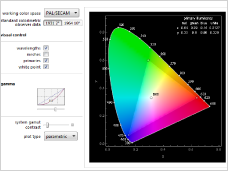 - Interactive graphics and animations: Mathematica
graphics are completely integrated into its dynamic interactivity
language. Any visualization can immediately be animated or made
interactive using a single command and developed into sophisticated,
dynamic visual applications.
© Copyright 2015 Wolfram Research.


|
|



