INTRODUCTION

This tutorial will explain the use of relational and logical operators in GAUSS.

 

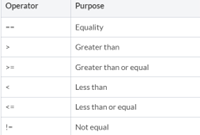
MATRIX RELATIONAL OPERATORS

• Return a scalar 1 if the statement is true for every element in the matrix, otherwise a 0.

SCALAR EQUALITY

a = 0.7;

// Set 'c1' equal to 1 if
 // 'a' is greater than 0.5
 c1 = a > 0.5;

// Set 'c2' equal to 1 if
 // 'a' is less than 0.5
 c2 = a < 0.5;

 

will assign

c1 = 1
c2 = 0

 

MATRIX INEQUALITY

In our first example, the variable a had only one element. Let’s look at a matrix example.

 // Create a 2x3 matrix
 a = { 0.1 0.5 0.4,
 0.5 0.3 0.7 };

// Assign 'c1' to equal 1 if EVERY
 // element of 'a' is > 0.4;
 c1 = a > 0.4;

// Assign 'c2' to equal 1 if EVERY
 // element of 'a' is < 0.8;
 c2 = a < 0.8;

 

will assign

c1 = 0
c2 = 1

 

This time, c1 will be set equal to 0, because several of the elements of a are less than 0.4.

 

Whereas c2 will be set equal to 1, because every element of a is less than 0.8.

 

MATRIX EQUALITY

 // Create a 2x3 matrix
 a = { 0.1 0.5 0.4,
 0.5 0.3 0.7 };

// Assign 'c1' to equal 1 if EVERY
 // element of 'a' is equal 0.4;
 c1 = a == 0.4;

// Assign 'c2' to equal 1 if EVERY
 // element of 'a' does NOT equal 0.4
 c2 = a != 0.4;

// Assign 'c3' to equal 1 if EVERY
 // element of 'a' does NOT equal 0.8
 c3 = a != 0.8;

 

After the code above:

c1 = 0
c2 = 0
c3 = 1

 

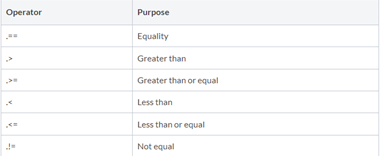
ELEMENT-BY-ELEMENT RELATIONAL OPERATORS

• Return a matrix or vector of 1’s and 0’s with a 1 at the location of the elements for which the operator returns true and a 0 for the other elements.

 

MATRIX ELEMENT‐BY‐ELEMENT INEQUALITY

The scalar case is the same as for the matrix operators, so we will start with a matrix example.

 // Create a 2x3 matrix
 a = { 0.1 0.5 0.4,
 0.5 0.3 0.7 };

// Return a 2x3 matrix of 1's
 // and 0's indicating whether the
 // corresponding element of 'a'
 // is > 0.4
 c1 = a .> 0.4;

// Return a 2x3 matrix of 1's
 // and 0's indicating whether the
 // corresponding element of 'a'
 // is ≤ 0.5
 c2 = a .<= 0.5;

 

After the above code

c1 = 0 1 0
     1 0 1
c2 = 1 1 1
     1 1 0

 

ExE CONFORMABILITY

The ExE conformability of the GAUSS relational operators makes it simple make comparisons along rows or columns.

 

COLUMN INEQUALITY

 // Create a 4x2 matrix
 a = { 125 23,
 150 31,
 105 19,
 150 33 };

// Create a 1x2 row vector
 b = { 120 25 };

// Check which elements in the first column of 'a'
 // are greater than the first element of 'b',
 // and which elements of the second column of 'a'
 // are greater than the second element of 'b'
 c = a .> b;

 

The above code will assign:

c = 1 0
    1 1
    0 0
    1 1

 

ROW INEQUALITY

  // Create a 4x2 matrix
 a = { 25 23,
 50 31,
 5 19,
 41 33 };

// Create a 4x1 column vector
 b = { 23,
 31,
 10,
 50 };

// Check which elements in the rows of 'a'
 // are less than or equal to the elements of the
 // corresponding row of 'b'
 c = a .<= b;

 

The above code will assign:

c = 0 1
    0 1
    1 0
    1 1

 

SCALAR LOGICAL OPERATORS

 

SCALAR ‘AND’

 a = 1;
 b = 9;
 x = 0;

// Are both 'a' and 'b' non-zero?
 c1 = a and b;

// Are both 'x' and 'a' non-zero?
 c2 = x and a;

// Are both 'b' and 0 non-zero?
 c3 = b and 0;

 

will assign

c1 = 1
c2 = 0
c3 = 0

 

SCALAR ‘OR’

 a = 1;
 b = 9;
 x = 0;

// Is either 'a' or 'b', or both, non-zero?
 c1 = a or b;

// Is either 'x' or 'a', or both, non-zero?
 c2 = x or a;

 

© 2024 Aptech Systems, Inc. All rights reserved.

 

  // Is either 'x' or 0, or both, non-zero?
 c3 = x or 0;

 

will assign

c1 = 1
c2 = 1
c3 = 0

 

SCALAR ‘NOT’

 a = 1;
 b = 9;
 x = 0;

// Is 'a' zero?
 c1 = not a;

// Is 'x' zero?
 c2 = not x;

// Does the expression (a and b) return zero?
 c3 = not (a and b);

 

will assign

c1 = 0
c2 = 1
c3 = 0 

 

ELEMENT-BY-ELEMENT RELATIONAL OPERATORS

 

ELEMENT-BY-ELEMENT ‘.AND’

Matrix and scalar case.

 a = { 1 2,
 3 0 };
 b = 9;
 x = 0;

// Are both 'a' and 'b' non-zero?
 c1 = a .and b;

// Are both 'a' and 'x' non-zero?
 c2 = a .and x;

 

will assign

c1 = 1 1
     1 0
c2 = 0 0
     0 0

 

Matrix and matrix case.

 a = { 1 2,
 3 0 };
 b = { 9 0,
 1 1 };

// Are both 'a' and 'b' non-zero?
 c1 = a .and b;

 

will assign

c1 = 1 0
     1 0

 

Matrix and row vector case.

 // 2x3 matrix
 a = { 1 0 8,
 0 3 1 };

// 1x3 row vector
 b = { 9 0 1 };

// Are the corresponding elements of 'a' and 'b' non-zero?
 c1 = a .and b;

 

will assign

c1 = 1 0 1
     0 0 1

 

Matrix and column vector case.

 // 3x3 matrix
 a = { 1 0 8,
 0 3 1,
 1 1 0 };

// 3x1 column vector
 b = { 2,
 1,
 0 };

// Are the corresponding elements of 'a' and 'b' non-zero?
 c1 = a .and b;

 

will assign

c1 = 1 0 1
     0 1 1
     0 0 0

 

ELEMENT-BY-ELEMENT ‘.OR’

Matrix and scalar case.

 a = { 1 2,
 3 0 };
 b = 9;
 x = 0;

// Are the elements of either 'a' or 'b', or both, non-zero?
 c1 = a .or b;

// Are the elements of either 'a' or 'x', or both, non-zero?
 c2 = a .or x;

 

will assign

c1 = 1 1
     1 1
c2 = 1 1
     1 0

 

Matrix and matrix case.

 a = { 1 2,
 3 0 };
 b = { 9 0,
 1 1 };

// Are the elements of either 'a' or 'b', or both, non-zero?
 c1 = a .or b;

 

will assign

c1 = 1 1
     1 1

 

Matrix and row vector case.

// 2x3 matrix
 a = { 1 0 8,
 0 3 1 };

// 1x3 row vector
 b = { 9 0 1 };

// Are the corresponding elements of either
 // 'a' or 'b', or both, non-zero?
 c1 = a .or b;

 

will assign

c1 = 1 0 1
     1 1 1

 

Matrix and column vector case.

// 3x3 matrix
 a = { 1 0 8,
 0 3 1,
 1 1 0 };

// 3x1 column vector
 b = { 2,
 1,
 0 };

// Are the corresponding elements of either
 // 'a' or 'b', or both, non-zero?
 c1 = a .or b;

 

will assign

c1 = 1 1 1
     1 1 1
     1 1 0

 

ELEMENT-BY-ELEMENT ‘.NOT’

 a = { 4 6,
 1 0,
 8 2 };

// Are the elements of 'a' zero?
 c1 = .not a;

 

will assign

c1 = 0 0
     0 1
     0 0