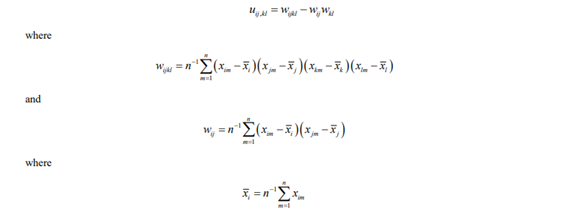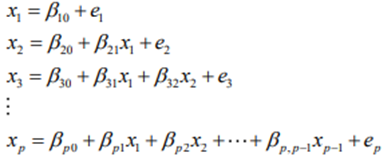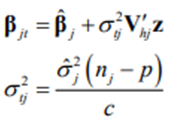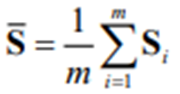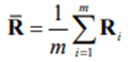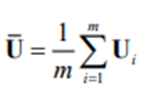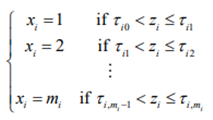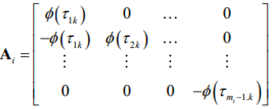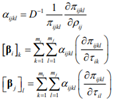During the last forty-five years, the LISREL model, methods and software have become synonymous with structural equation modeling (SEM). SEM allows researchers in the social sciences, management sciences, behavioral sciences, biological sciences, educational sciences and other fields to empirically assess their theories. These theories are usually formulated as theoretical models for observed and latent (unobservable) variables. If data are collected for the observed variables of the theoretical model, the LISREL program can be used to fit the model to the data.
Today, however, LISREL is no longer limited to SEM. LISREL 12 includes the 64-bit statistical applications LISREL, PRELIS, MULTILEV, SURVEYGLIM and MAPGLIM.
|
LISREL is a 64-bit application for standard and multilevel structural equation modeling. These methods are available for the complete and incomplete complex survey data on categorical and continuous variables as well as complete and incomplete simple random sample data on categorical and continuous variables.
MULTILEV is a 64-bit application that fits multilevel linear and nonlinear models to multilevel data from simple random and complex survey designs. It allows for models with continuous and categorical response variables.
MGLIM is a 64-bit application that uses adaptive quadrature to fit generalized linear models with categorical, count and non-normally distributed outcome variables to multilevel data.
|
PRELIS is a 64-bit application for data manipulation, data transformation, data generation, computing moment matrices, computing estimated asymptotic covariance matrices of sample moments, imputation by matching, multiple imputation, multiple linear regression, logistic regression, univariate and multivariate censored regression, and ML and MINRES exploratory factor analysis.
SURVEYGLIM is a 64-bit application that fits Generalized LInear Models (GLIMs) to data from simple random and complex survey designs. Models for the Multinomial, Bernoulli, Binomial, Negative Binomial, Poisson, Normal, Gamma, and Inverse Gaussian sampling distributions are available. |
Several special features and improvements are available in LISREL. Observed and latent variable names of up to sixteen characters are permitted and path diagram files can be exported as enhanced metafiles which can be imported into other documents. HTML tables for the various results of single group LISREL models are provided in the form of a HTML file. The iterative estimation algorithm for the parameters of LISREL models, which uses adaptive quadrature, has been improved. The multilevel generalized linear modeling application includes more link functions and computes estimates of the intra-class correlation coefficients.
LISREL also includes several new statistical methods. More specifically, two-stage multiple imputation Structural Equation Modeling (SEM) for continuous, ordinal, and a mixture of continuous and ordinal variables, confidence interval estimates for the parameters of LISREL models, and standard error estimates and confidence interval estimates for standardized and completely standardized solutions are implemented. In addition, an alternative iterative estimation algorithm for the parameters of the general LISREL model and the extended LISREL model is available.
The technical details along with illustrative examples for two-stage multiple imputation SEM are provided in section 1. Section 2 contains the statistical theory for standard error and confidence interval estimates for the parameters of LISREL models and includes an illustrative example. In section 3, the estimation theory for estimating the parameters of single group LISREL models with variance constraints for the endogenous latent variables is provided and demonstrated. The GaussNewton algorithm for estimating the parameters of the extended LISREL model is described and illustrated in section 4.
The following features are new in Lisrel 12
| TWO STAGE MULTIPLE IMPUTATION SEM
CONTINUOUS VARIABLES
MOMENT MATRICES
Suppose that the rows of X (n x p) are n observations of p continuous variables x1, x2,…, xp with mean vector μ and covariance matrix Σ . The sample covariance matrix, S , is an unbiased estimator of Σ and may be expressed as
where xi and ¯x denote observation i and the sample mean vector of x =
The robust ML, DWLS, WLS, and ULS methods can be used to fit structural equation models for continuous variables to the sample covariance matrix by using the estimated asymptotic covariance matrix of the sample variances and covariances.
The correlation matrix, P, x1, x2,…, xp is the covariance matrix of the standardized variables z1, z2,…, zp where
and
where Dσ denotes a diagonal matrix with the standard deviations σ1,σ2,…, σp of x1, x2,…, xp on the diagonal. The sample correlation matrix, R, is an unbiased estimator of P and may be expressed as
where Ds denotes a diagonal matrix with the sample standard deviations s1,s2,…, sp of x1,x2,…, xp on the diagonal. A typical element of a consistent estimator, U, of the asymptotic covariance matrix, ϒ, of the sample correlations (Steiger and Hakstian 1982) is given by
where
and
and
The robust DWLS, WLS, and ULS methods can be used to fit structural equation models for continuous variables to the sample correlation matrix by using the estimated asymptotic covariance matrix of the sample correlations.
MULTIPLE IMPUTATION
The MCMC method Suppose now that the n observations of the p continuous variables include missing data values with k missing data value patterns and that the joint distribution of the variables is a multivariate normal distribution with mean vector μ and covariance matrix Σ. The EM algorithm and the MCMC method for multiple imputation of incomplete data can be used to impute the missing data values of the continuous variables.
Suppose that Xo denote the observed data values. The EM algorithm (Dempster, Laird, and Rubin 1977) can be used to compute the maximum likelihood estimate of Σ. The minus two observed-data log likelihood may be expressed as
where ni denotes the number of observations of missing data value pattern i = 1,2,…, k, Σi denotes the population covariance matrix of missing data value pattern i, μi denotes the mean vector of missing data value pattern i, and xoij is the jth vector of observed values of missing data value pattern i.
The initial estimate for the M-step is the sample covariance matrix, S, of the complete data or Ip if the number of complete observations is too small. In the E-step, the conditional covariance matrices of the missing variables given the observed variables of the missing data value patterns are computed and used to compute an updated estimate
The EM estimate, Σˆ, of Σ is used as the initial covariance matrix of the multivariate normal distribution in the first step of the Monte Carlo Markov Chain (MCMC) method. In the first step (P-step) of the MCMC method, an estimate of Σ is simulated from an inverse Wishart distribution. In the I-step, observations are simulated from the conditional normal distributions of the missing variables given the observed k missing data value patterns and used to replace the missing data values. The next estimate of Σ is then obtained by computing the sample covariance matrix of the completed data. The P and I steps are repeated for a fixed number of times.
The FCS regression method
Suppose now that the n observations of the p continuous variables include missing data values and that a joint (multivariate) distribution of the variables exists. In this case, the Fully Conditional Specified (FCS) regression method (Brand 1999; Van Buuren 2007) can be used to impute the missing data values. The FCS regression method performs a fixed number of imputations to impute the missing data values. Each imputation consists of a filled-in phase and an imputation phase. In the filled-in phase, the missing data values are filled-in by using a sequence of regression analyses for the p continuous variables. These filled-in data are then used as the initial data for the imputation phase in which the missing data values are imputed by using a sequence of regression analyses for the p continuous variables. These imputed data are then used as the initial data for the next iteration of the imputation phase and a fixed number of iterations are executed for each imputation.
The filled-in stage fits the following p regression models sequentially to the data, namely
where the elements of β = For each iteration of the imputation stage, the following regression models are fitted sequentially either to the filled-in data or the imputed data, namely
where j = 1,2,…, p, the elements of βj =
where X(j) denotes rows 1,2,…, j-1, j,…, p of the filled-in or imputed data. New values for the parameters are then simulated from their posterior distributions as
where Vhj denotes the upper triangular matrix in the Cholesky decomposition of Vj =V’hj Vhj, z denotes a p x 1 standard normal vector, and c is a Chi-square variable with nj – p degrees of freedom. The missing data values are then imputed as
where xijm denotes a missing data value in row i and column j of X, xi(j) denotes row i of X(j), and z is a standard normal variable.
Average unstandardized moment matrices
Suppose that X1,X2,…,Xm are m imputed data sets for the incomplete data matrix, X, of the p continuous variables x1,x2,…, xp and that S1,S2,…, Sm and U1,U2,…, Um denote the corresponding sample covariance matrices and the estimated asymptotic covariance matrices of the variances and covariances, respectively. Then, the average sample covariance matrix is
and the average estimated asymptotic covariance matrix is
|
Chung and Cai (2019) point out that Ū only captures uncertainty based on complete data. As a result, its inverse cannot be used as a weight matrix for the robust ML, DWLS, WLS, and ULS methods for continuous structural equational modeling. A corrected weight matrix is obtained by correcting for the between-imputation variation in the estimated variances and covariances and is obtained as the inverse of
where sdenotes the p x (p+1)/2 vector consisting of the nonduplicated elements of the p x p symmetric matrix S. S̄ and ϒ can be used to fit structural equation models to the average sample covariance matrix with the robust ML, DWLS, WLS, and ULS methods. The corrected robust DWLS and ULS Chi-square test statistic proposed by Chung and Cai (2019) is given by
where
where Δ denotes the Jacobian matrix of σ(θ) with respect to the unknown parameters θ of the structural equation model evaluated at θ=θ. The small sample adjusted Tb test statistic (Yuan and Bentler 1997) is given by
Average standardized moment matrices
Suppose that X1,X2,…,Xm are m imputed data sets for the incomplete data matrix, X, of the p continuous variables x1,x2,…, xp and that R1,R2,…, Rm and U1,U2,…, Um denote the corresponding sample correlation matrices and the estimated asymptotic covariance matrices of the sample correlations, respectively. Then, the average sample correlation matrix is
and the average estimated asymptotic covariance matrix is
Chung and Cai (2019) point out that Ū only captures uncertainty based on complete data. As a result, its inverse cannot be used as a weight matrix for the robust DWLS, WLS, and ULS methods for continuous structural equational modeling for correlation matrices. A corrected weight matrix is obtained by correcting for the between-imputation variation in the estimated correlations and is obtained as the inverse of
where r denotes the p x (p-1)/2 vector consisting of the nondiagonal and the nonduplicated elements of the p x p symmetric matrix R. R̄ and ϒ can be used to fit structural equation models to the average sample correlation matrix with the robust DWLS, WLS, and ULS methods. The corrected robust DWLS and ULS Chi-square test statistic proposed by Chung and Cai (2019) is given by
where
where Δ denotes the Jacobian matrix of p (θ) with respect to the unknown parameters θ of the structural equation model evaluated at θ=θ. The small sample adjusted Tb test statistic (Yuan and Bentler 1997) is given by
ORDINAL VARIABLES
Polychoric Correlations
Suppose that the rows of X (nxp) are n observations of p ordinal variables x1,x2,…, xp with m1,m2,…, mp categories, respectively. Suppose further that these p ordinal variables are the result of the discretization of the underlying p continuous standard normal variables z1,z2,…, zp as such that z =
where P denotes the population correlation matrix of z and
where ∅ (.) denotes the probability density function of the standard normal distribution. The maximum likelihood estimator of
where Φ -¹ denotes the inverse of the cumulative distribution function of the standard normal distribution and pi1, pi2,…, pimi denote the marginal sample proportions for xi.
The polychoric correlation matrix, R, is a consistent estimator of the population correlation matrix P. The model for the bivariate marginal of variables xi and xj is
where ∅2 (u,v, pij) denotes the probability density function of the bivariate standard normal distribution with correlation pij. The maximization of the bivariate likelihood function is equivalent to minimization of the discrepancy function
where
where (Olsson 1979)
where ∅2 (.) denotes the density function of the bivariate standard normal distribution with correlation pij. The information (Jöreskog, 1994) is given by
The Fisher scoring algorithm is used to minimize F (.) with respect to pij . Let θ= pij . If
Iteration is terminated when the absolute gradient value is below the tolerance limit ε=10-³.
The asymptotic covariance matrix, ϒ, of the p* = p(p-1)/2 polychoric correlations is a p*(p*+1)/2 matrix. A typical element of ϒ (Jöreskog, 1994) may be expressed as
where
where 1i denotes an mi x 1 column vector and
where Ai denotes the mi x (mi – 1) matrix given by
Typical elements of αij, βi, and βj are given by
where
The robust DWLS, WLS, or ULS methods can be used to fit structural equation models for ordinal variables to the polychoric correlation matrix by using the estimated asymptotic covariance matrix of the polychoric correlations (Chung and Cai (2019)). |
The Software includes product activation designed to prevent unauthorized use and copying. This technology may cause your computer to automatically connect to the Internet and may prevent uses of the Software that are not permitted. Do not activate the Software provided under this license agreement (“Agreement”), until you have carefully read this Agreement. By activating the Software, using the activation code provided, you agree to be bound by the terms and conditions of this Agreement. If you do not agree to the terms and conditions of this Agreement, do not activate the Software. The effective date for this Agreement shall be the day you activate the licensed Software. You may have another agreement with SSI that supplements or supersedes all or portions of this Agreement.
Scientific Software International, Inc. (‘SSI’) grants to licensee the non-exclusive, non-transferable right to download, install, use, or otherwise benefit from the functionality or intellectual property of the copyrighted Software only in accordance with the terms of this Agreement. This license will continue for the specified duration or in perpetuity unless you violate the terms below or destroy all your copies of the Software. You may not sell, rent, or lease this license. The term ‘Software’ includes all computer code, activation codes and other materials, including any updates and upgrade thereto, that are provided to you under this Agreement.
SCOPE AND DURATION
The scope and duration (time period) of your license depends on the type of license you obtained from SSI, as specified in the accompanying invoice. The various license types are set forth below.
I SINGLE USER LICENSE
A single user license permits activation on one computer for one specific end user and is a perpetual license.
II CONCURRENT USER LICENSE
Multiple concurrent user licenses permit activations on multiple computers for multiple end users. If the number of computers and the number of different end users exceed the number of concurrent user licenses, license metering software is required to restrict the simultaneous access to the Software to the number of concurrent user licenses.
A fixed number (n) of concurrent user licenses permits activations on n computers for any number of different end users.
An individual concurrent user license for one specific end user permits the end user activations on multiple computers as long as the specific end user is the only end user of the Software on all the computers involved.
Concurrent user licenses are perpetual licenses.
III RENTAL LICENSE
A rental license permits activation on one computer for one specific end user and expires either 183 days or 365 days after activation.
IV SINGLE 12 MONTH NON-ACADEMIC LICENSE
A single 12 month non-academic license permits activation on one computer for one specific end user and expires 365 days after activation.
GENERAL TERMS
Title to the Software and all copies thereof remain with SSI and its suppliers. The Software is licensed, not sold. The Software is copyrighted and is protected by United States copyright laws and international treaty provisions. You will not remove any copyright notice from the Software. You agree to prevent any unauthorized copying of the Software. Except as expressly provided herein, no license or right is granted to you directly or by implication, inducement, estoppel, or otherwise, specifically SSI does not grant any express or implied right to you under SSI patents, copyrights, trademarks, or trade secret information. You may not reverse engineer, disassemble, decompile, or otherwise attempt to discover the source code of the Software.
SSI agrees to respond to brief technical questions received via email from end users with active licenses. The Software is guaranteed to replicate output generated from sample files provided with the Software. SSI reserves the right to determine if and/or when an error in Software coding exists, as well as when, how, and whether you will be sent a refund or a free correction. SSI warrants that the Software does not infringe any patent, trademark, trade secret, copyright, or other proprietary right of any other person or entity. Except as set forth herein, the Software is supplied without warranty of any kind, expressed or implied, including but not limited to the implied warranties of merchantability and fitness for a particular purpose. Neither SSI nor the author of the Software warrant that the functions contained in the Software will meet customer’s requirements or that operation of the Software will be error free and/or without Interruption.
In no event will SSI be liable to you for any damages, including any lost profits, lost savings, or other incidental or consequential damages arising out of the use of or the inability to make use of the Software, even if SSI has been advised of the possibility of such damages, or for any other claim by any other party. This Agreement is intended to be the entire agreement between you and SSI with respect to matters contained herein, and supersedes all prior or contemporaneous agreements and negotiations with respect to those matters. No waiver of any breach or default shall constitute a waiver of any subsequent breach or default. If any provision of this Agreement is determined by a court to be unenforceable, you and SSI will deem the provision to be modified to the extent necessary to allow it to be enforced to the extent permitted by law, or if it cannot be modified, the provision will be severed and deleted from this Agreement, and the remainder of the Agreement will continue in effect. Any change, modification or waiver to this Agreement must be in writing and signed by an authorized representative of you and SSI.
MICROSOFT WINDOWS
SYSTEM REQUIREMENTS
- Operating System: Windows 7/8/8.1/10
- Memory (RAM): 1 GB of RAM required.
- Hard Disk Space: 100 MB of free space required.
- Processor: Intel Pentium 4 or later.
NOTE:
Currently Lisrel offers no native Mac version of any of our programs currently available. However, if you have a dual-boot set-up or a Windows emulator, any of our programs should run without issues. Note that Lisrel can only provides support for using the software and are unable to provide guidance on setting up a Mac to allow for a program to be usable. Parallels Desktop is the most frequently used of the emulators. VirtualBox is a free alternative from Oracle, but it can be very slow compared to Parallels.
TECHNICAL DOCUMENTS
GUIDES:
ADDITIONAL MULTILEVEL MATERIAL NOT CONTAINED IN THE MULTILEVEL MODELING GUIDE:
© 2025 Scientific Software International, Inc.
Software originalmente sviluppato per la stima di modelli di equazioni strutturali (SEM). Oggi comprende molte altre applicazioni statistiche.